§5.7
广义积分
【引例】计算曲线 ![]() 与
与![]() 轴的正半轴所围的曲边梯形的面积。
轴的正半轴所围的曲边梯形的面积。
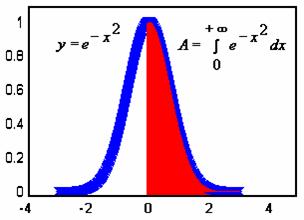
按照定积分的几何意义,所求的曲边梯形面积应为
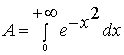 。
。
显然,这一积分再不是普通的定积分,因为它的积分上限是正无穷大。
该如何来求这一“新定积分”的值呢?首先用计算机来做一个数值试验:
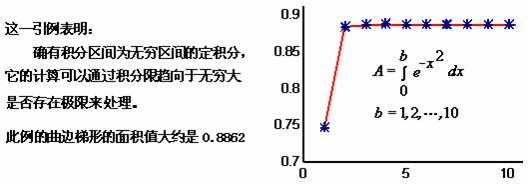
编程计算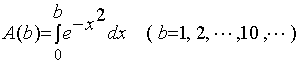 的值,并作出这些值的图象,观察图象是否逼近于一条固定的直线。
的值,并作出这些值的图象,观察图象是否逼近于一条固定的直线。
请运行matlab程序gs0504.m。
一、积分区间为无穷区间的广义积分
【定义一】
设函数![]() 在区间
在区间![]() 上连续, 任取
上连续, 任取 ![]() ,如果极限
,如果极限
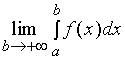
存在,则称此极限值为函数![]() 在无穷区间
在无穷区间![]() 上的广义积分,并记作
上的广义积分,并记作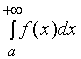 ,亦即
,亦即

此时,也称广义积分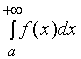 收敛;
收敛;
如果上述极限不存在,
则称广义积分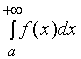 发散。
发散。
类似地
设函数![]() 在区间
在区间![]() 上连续,任取
上连续,任取 ![]() ,如果极限
,如果极限
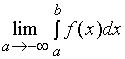
存在,则称此极限值为函数![]() 在无穷区间
在无穷区间![]() 上的广义积分,
上的广义积分,
记作  ,亦即
,亦即
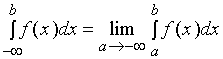
此时,也称广义积分
 收敛;如果上述极限不存在,
则称广义积分
收敛;如果上述极限不存在,
则称广义积分 发散。
发散。
类似地
设函数![]() 在区间
在区间![]() 上连续,如果广义积分
上连续,如果广义积分
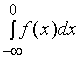 与
与 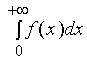
同时收敛,则称上述两广义积分之和为函数![]() 在无穷区间
在无穷区间![]() 上的广义积分,记作
上的广义积分,记作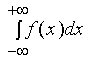 。
。
亦即
 这时,也称广义积分
这时,也称广义积分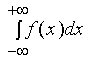 收敛;如果上述极限不存在,则称广义积分
收敛;如果上述极限不存在,则称广义积分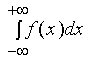 发散。
发散。
上述积分称为无穷限的广义积分。

【反例】 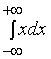

但

 发散,因此,
发散,因此,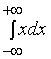 是发散的。
是发散的。
【例1】计算广义积分 
解:
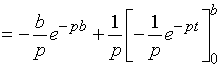
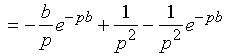

显然,无穷限广义积分就是任意有限区间上定积分的极限。
【例2】计算广义积分  。
。
解:

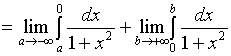
![]()
![]()
![]()
![]()
观察上述解题过程,极限符号直到最后才参与运算,为了方便,我们可以将之写成如下形式:
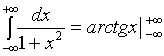
请注意:将上下限![]() 代入原函数时,意味着取极限
代入原函数时,意味着取极限
![]()
这样约定,并未改变无穷限广义积分的实质,却使记号简洁了许多,且与定积分的计算程序基本上一致。
【例3】证明广义积分 当
当 ![]() 时收敛; 当
时收敛; 当![]() 发散。
发散。
解:若
![]()
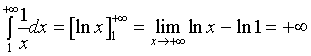
若 ![]()

二 无界函数的广义积分
【定义二】
设函数![]() 在区间
在区间![]() 上连续, 且
上连续, 且![]() ,取
,取 ![]() ,
,
如果极限 存在,则称此极限值为函数
存在,则称此极限值为函数![]() 在区间
在区间![]() 上的广义积分,记作
上的广义积分,记作  。亦即
。亦即
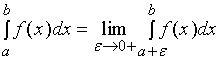
此时,也称广义积分 收敛;如果上述极限不存在,则称广义积分
收敛;如果上述极限不存在,则称广义积分 发散。点
发散。点![]() 称之为奇点。
称之为奇点。
类似地,有
设函数![]() 在区间
在区间![]() 上连续,且
上连续,且![]() ,取
,取 ![]() ,如果极限
,如果极限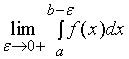 存在,则称此极限值为函数
存在,则称此极限值为函数![]() 在区间
在区间![]() 上的广义积分,记作
上的广义积分,记作  。亦即
。亦即
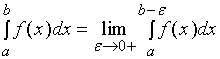
此时,
也称广义积分 收敛;如果上述极限不存在, 则称广义积分
收敛;如果上述极限不存在, 则称广义积分 发散。点
发散。点 ![]() 称之为奇点。
称之为奇点。
类似地,
又有
设函数![]() 在
在![]() 上除
上除![]() 外均连续, 且
外均连续, 且![]() ,
,
如果两个广义积分
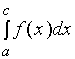 与
与 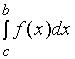 均收敛, 则定义广义积分
均收敛, 则定义广义积分

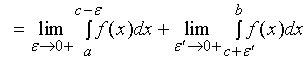
否则称广义积分 发散。点
发散。点 ![]() 称之为奇点
称之为奇点
注明:上式中的![]() 与
与![]() 不一定是相同的。
不一定是相同的。
【例4】求 
解: ,
,
故 ![]() 奇点。
奇点。

注明:为了简便,上述过程也可写成
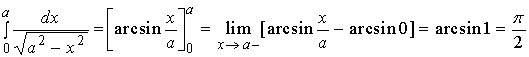
【例5】讨论![]() 的敛散性。
的敛散性。
解: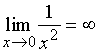 ,故
,故 ![]() 是奇点。
是奇点。

故
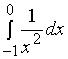 发散,从而, 原广义积分
发散,从而, 原广义积分 亦发散。
亦发散。
此题若忽视![]() 是奇点,将积分当作普通积分来处理,会导致错误解法
是奇点,将积分当作普通积分来处理,会导致错误解法

【例6】证明广义积分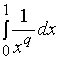 当
当![]() 时收敛;当
时收敛;当![]() 时发散。
时发散。
解:当
![]() 时,
时, ![]() 是奇点,
是奇点,
广义积分
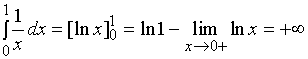 ,
,
故广义积分
 发散;
发散;
当![]() 时,
时,

故广义积分
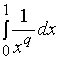 收敛;
收敛;
当![]() 时,
时,

故广义积分
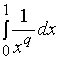 发散;
发散;
综合得:
